The Overlord of the Über-Feral says: Welcome to my bijou bloguette. You can scroll down to sample more or simply:
• Read a Writerization at Random: RaWaR
• ¿And What Doth It Mean To Be Flesh?
Gweel & Other Alterities – Incunabula’s new edition
Tales of Silence & Sortilege – Incunabula’s new edition
If you’d like to donate to O.o.t.Ü.-F., please click here.
I identify as √-37 (the square root of -37) in bases 5 (on Mondays and Wednesdays), 17 (Tuesdays, Thursdays and alternate Saturdays) and 89 (Fridays, Sundays and alternate Saturdays).
My preferred pronouns are 6.08276i, 雲 and მსოფლიოს მეფე.
(animated rainbow flag courtesy dribble.com)
“Descending Toward the Moon” (1951) by Chesley Bonestell (1888–1986)
As Reform seeks a statement victory in Gorton and Denton, with a candidate who has made dog-whistle nativism his calling card, Manchester has again become a political crucible. […] As Nigel Farage’s intellectual outriders speak of a “politics of home”, which casts doubt over certain citizens’ right to be considered British, a billionaire tax exile in Monaco has added grist to their mill. — “Guardian view on Sir Jim Ratcliffe: Britain does not need political lectures from a billionaire tax exile”, The Guardian, 12ii26
This is the surpassingly special Stern-Brocot sequence:
0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, … (A002487 at the Online Encyclopedia of Integer Sequences)
And why is the sequence special? Because if you take successive pairs of the apparently arbitrarily varying numbers, you get every rational fraction in its simplest form exactly once. So 1/2, 2/3, 6/11 and 502/787 appear once and then never again. And so do 2/1, 3/2, 11/6 and 787/502. Et cetera, ad infinitum. If you map the Stern-Brocot sequence against the related Calkin-Wilk sequence, which has the same “all-simplest-fractions-exactly-once” properties, you can create this fractal, which I call a limestone fractal or gryke fractal:
Gryke fractal by mapping Stern-Brocot sequence against Calkin-Wilf sequence
The graph is what I call a Fract-L, because the lines for the x,y coordinates create an L. Each coordinate runs from 0 to 1, with the x set by the fraction from the Stern-Brocot sequence and the y set by the fraction from the Calkin-Wilf sequence (if a > b in a/b, use the conversion 1/(a/b) = b/a). But you can also find interesting patterns by mapping the Stern-Brocot sequence against itself. That is, you use two Stern-Brocot sequences that start in different places. Now, there are complicated ways to create the Stern-Brocot sequence using mathematical trees and sequential algorithms and so on. But there’s also an astonishingly simple way, a formula created by the Israeli mathematician Moshe Newman. If (a,b) is one pair of successive numbers in the sequence, the next pair (a,b) is found like this:
c = b
b = (2 * int(a/b) + 1) * b – a
a = c
This means that you can seed a Stern-Brocot sequence with any (correctly simplified) a/b and it will continue in the right way. If the two SB-sequences for x and y are both seeded with (0,1), you get this 45° line, because each successive a/b for (x,y) is identical:
Stern-Brocot pairs seeded with x ← (0,1) and y ← (0,1)
The further you extend the sequences, the less broken the 45° line will appear, because the points determined by a/b for x and y will get closer and closer together (but the line will never be solid, because any two rationals are separated by an infinity of irrationals). Now try offsetting the SB-sequences for x,y by using different seeds. Different fractal patterns appear, which all appear to be subsets (or fractions) of the limestone fractal above (see animated gif below):
Stern-Brocot pairs seeded with x ← (0,1) and y ← (1,1)
x ← (0,1) and y ← (1,2)
x ← (0,1) and y ← (1,3)
x ← (0,1) and y ← (2,3)
x ← (0,1) and y ← (3,4)
x ← (0,1) and y ← (6,7)
x ← (1,2) and y ← (1,9)
x ← (1,4) and y ← (1,6)
x ← (1,7) and y ← (1,8)
x ← (2,3) and y ← (4,5) — apparently identical to x ← (1,4) and y ← (1,6) above
x ← (26,25) and y ← (1,10)
Gryke fractal compared with Stern-Brocot-pair patterns (animated at ezGif)
And here’s what happens when the seed-fractions for x run from 1/3 to 12/13, while the seed-fraction for y is held constant at 1/23:
x ← (1,13) and y ← (1,23)
x ← (2,13) and y ← (1,23)
x ← (3,13) and y ← (1,23)
x ← (4,13) and y ← (1,23)
x ← (5,13) and y ← (1,23)
x ← (6,13) and y ← (1,23)
x ← (7,13) and y ← (1,23)
x ← (8,13) and y ← (1,23)
x ← (9,13) and y ← (1,23)
x ← (10,13) and y ← (1,23)
x ← (11,13) and y ← (1,23)
x ← (12,13) and y ← (1,23)
Animated gif for x ← (n,13) and y ← (1,23) (animated at ezGif)
Previously Pre-Posted
• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the fractal
Like mine, the veins of these that slumber
Leapt once with dancing fires divine;
The blood of all this noteless number
Ran red like mine.
How still, with every pulse in station,
Frost in the founts that used to leap,
The put to death, the perished nation,
How sound they sleep!
These too, these veins which life convulses,
Wait but a while, shall cease to bound;
I with the ice in all my pulses
Shall sleep as sound.
• A.E. Housman, “XX” in More Poems (1936)
Elsewhere Other-Accessible…
Serendipity in some simplification statistics. That’s what I encountered the other day. I was looking at the ways to simplify this set of fractions:
1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, 3/6, 4/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 1/11, 2/11, 3/11, …
The underlined fractions are not in their simplest possible form. For example, 2/4 simplifies to 1/2, 2/6 to 1/3, 3/6 to 1/2, and so on:
1/2, 1/3, 2/3, 1/4, 2/4 → 1/2, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6 → 1/3, 3/6 → 1/2, 4/6 → 2/3, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8 → 1/4, 3/8, 4/8 → 1/2, 5/8, 6/8 → 3/4, 7/8, 1/9, 2/9, 3/9 → 1/3, 4/9, 5/9, 6/9 → 2/3, 7/9, 8/9, 1/10, 2/10 → 1/5, 3/10, 4/10 → 2/5, 5/10 → 1/2, 6/10 → 3/5, 7/10, 8/10 → 4/5, 9/10, 1/11, 2/11, 3/11, …
I counted the number of times the simplest possible fractions occurred when simplifying all fractions a/b for (b = 2..n, a = 1..b-1), then displayed the stats as a graph running from 0/1 to 1/1. And there was serendipity in these simplification statistics, because a fractal had appeared:
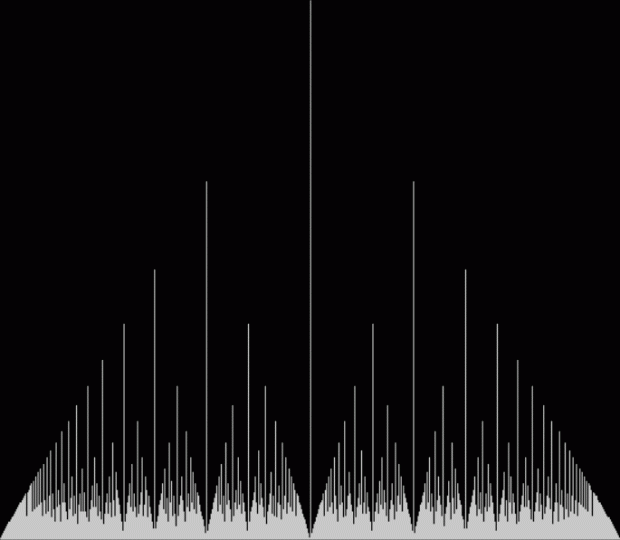
Graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)
It’s interesting to work out what fractions appear where. For example, the peak in the middle is 1/2, but what are the next-highest peaks on either side? The answers are more obvious in the colored version of the graph:
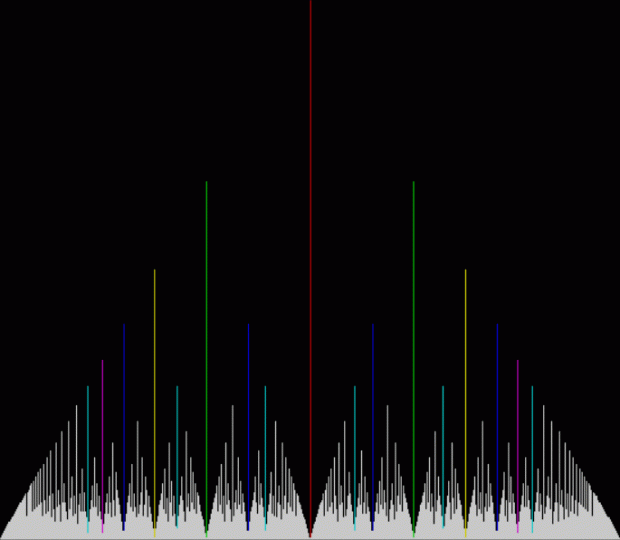
Colored graph for count of simplest possible fractions
Key: n/2, n/3, n/4, n/5, n/6, n/7
The line for 1/2 is red, the lines for 1/3 and 2/3 in light green, the lines for 1/4 and 3/4 in yellow, and so on. But those graphs appear in an equilateral triangle, as it were. The fractals get easier to see in the full-sized versions of these widened graphs:
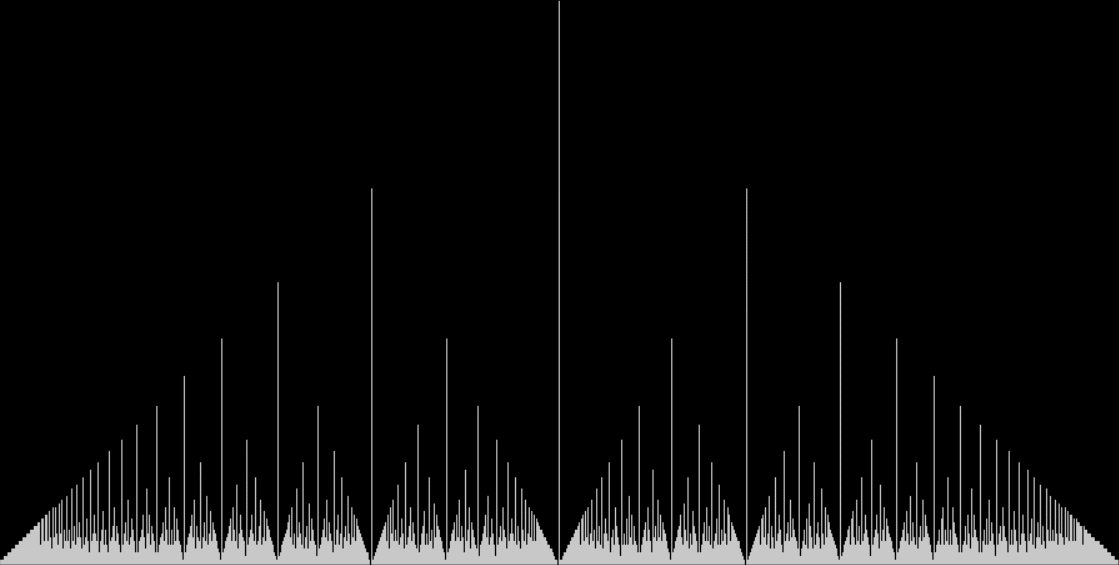
Widened graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)
(click for full size)
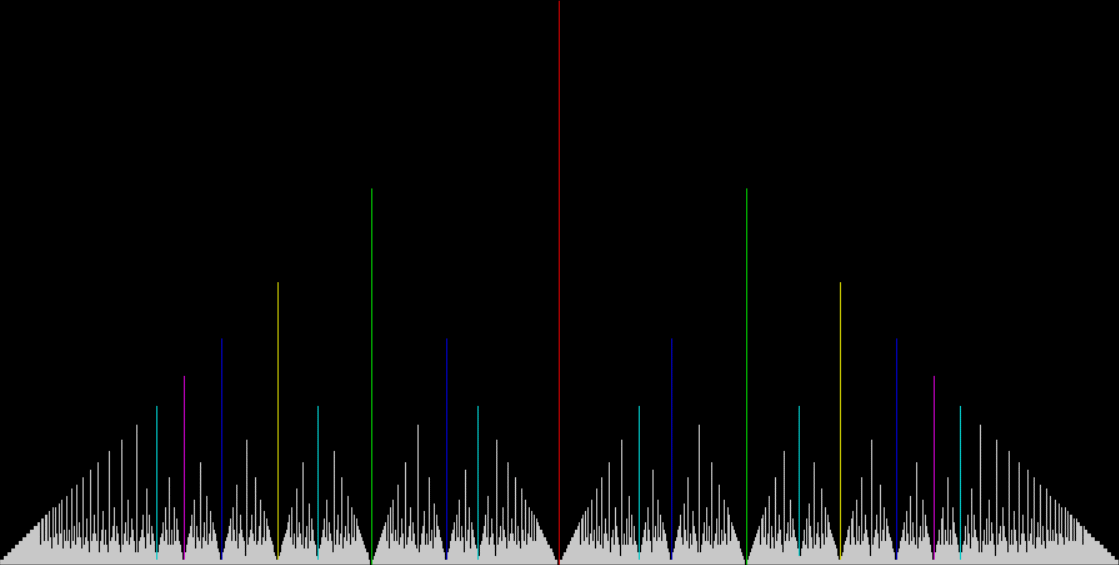
Widened and colored graph for count of simplest possible fractions
(click for full size)
In the wake of the spread of Protestantism, the literacy rates in the newly reforming populations in Britain, Sweden, and the Netherlands surged past more cosmopolitan places like Italy and France. Motivated by [the demands of] eternal salvation, parents and leaders made sure the children learned to read. […] The Protestant impact on literacy and education can still be observed today in the differential impact of Protestant vs. Catholic missions in Africa and India. In Africa, regions with early Protestant missions at the beginning of the Twentieth Century (now long gone) are associated with literacy rates that are about 16 percentage points higher, on average, than those associated with Catholic missions. In some analyses, Catholics have no impact on literacy at all unless they faced direct competition for souls from Protestant missions. These impacts can also be found in early twentieth-century China.
Saturn through a 6″ telescope (Reddit)
“Our fantastic civilization has fallen out of touch with many aspects of nature, and with none more completely than with night. Primitive folk, gathered at a cave mouth round a fire, do not fear night; they fear, rather, the energies and creatures to whom night gives power; we of the age of the machines, having delivered ourselves of nocturnal enemies, now have a dislike of night itself. With lights and ever more lights, we drive the holiness and beauty of night back to the forests and the sea; the little villages, the cross-roads even, will have none of it. Are modern folk, perhaps, afraid of night? Do they fear that vast serenity, the mystery of infinite space, the austerity of stars?” — Henry Beston (1888-1968), The Outermost House, 1933
Christ Carrying the Cross by Hieronymus Bosch or follower, Ghent (1510-35)
• Et que signifie donc d’être chair ?
• Und was heißt es, Fleisch zu sein?
• E che vuol dire essere carne?
• ¿Y qué quiere decir ser carne?
• और देह होना आखिर क्या है?
• და რას ნიშნავს ხორცად ყოფნა?
• 而为肉身，究竟意味着什么？
• अथ मांसत्वं किमर्थम्?
• ⲁⲩⲱ ⲧⲓ ⲟⲩⲛ ⲡⲉ ⲡⲓⲥⲁⲣⲝ ⲉⲧⲙⲉ?
• 𒅇 𒍑𒆪 𒅆𒂟 𒅗?
Ego non sum…
Evangelium secundum Ioannem XVII, xiv.
The old palace had a thousand corridors, ten thousand mirrors, squares, ovals, and diamonds, which remained bright and clear for all the dust and cobwebs that surrounded them, specking not with the autumn rain that fell through rents in the roof, cracking not in the fierce frosts of midwinter, ever fascinating, ever fearful to the youths and maidens of the villages therearound. For no mirror reflected faithfully, or so ’twas said, having always some sorcerous taint or anomaly, whereby, on early corridors, the faces reflected were not quite those of him or her who stood before them, being distinct in some particular of eye or mouth or cheek, of hair or tint or scarring, as though a brother or sister looked out, not a twin; and on later the faces reflected began to alter more strongly, more unsettlingly, seeming to partake of different nation and race; and on last of all, seen by very few, the faces reflected began to depart the bounds of humanity, borrowing form and feature from beasts, birds, and fish.
But horrider than these, found here and there in the palace, were mirrors wherein viewers saw themselves become giant insects, myriad-eyed, with nodding antennæ, finger-like jaws or coiled proboscis, or else arachnids, crustaceans, or worms, whereat some fled in horror or fainted where they stood, and few indeed could watch the transformations for long. Kinder mirrors might stand a stride or two away, natheless, wherein faces became now flowers, great and glorious, now crystals of many and gorgeous facets or polyhedra of polished metal, reflective themselves within a reflection. But these mirrors too could trouble the brain and linger in dreams, being sorcerous equally with the rest, nor did it seem right that fragrance should leak from the flowers and notes chime from the crystals and polyhedra. Wherefor no mirror in the old palace could be viewed with impunity, save by the dullest-witted, the stupidest, and these too feared to come before one or another of two mirrors said to be horriblest of all.
In one of these, the viewer would see himself seemingly true at first, then note that months were passing in the mirror for moments before it, whereby one aged before one’s very eyes, skin wrinkling, nose expanding, jaw collapsing. And if one watched unwisely long, one saw death possess the face and a haze of maggots eat it to bare and grinning bone.
In the other of these mirrors, the viewer saw somewhat more disturbing still, save to a rarest few: namely, naught at all where a face should have looked back, as though one existed not and the world flowed on unaffected.
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 